CSAPP 第三章主要以理解 C 语言编译器产生的汇编代码为目的,简要介绍了 x86-64 汇编。
3.4 访问信息

可以看到对应函数调用的前 6 个参数的寄存器分别是 %rdi,%rsi,%rdx,%rcx,%r8,r9。
3.5 算术和逻辑操作
下表列出了 x86-64 的一些算术和逻辑操作指令。除 leaq 外,大多数操作都分成了指令类,各自带有不同大小操作数的变种(如 add 分为 addb, addw, addl, addq 四个变种)。这些指令被分为四类:加载有效地址、一元操作、二元操作、移位。
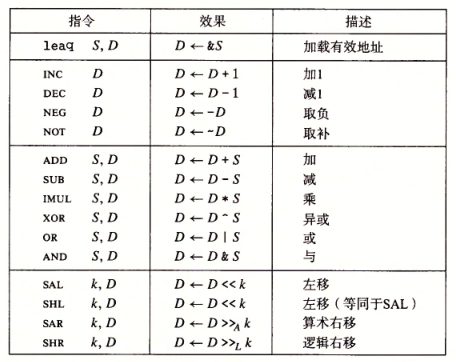
3.5.1 加载有效地址
leaq (load effective address,加载有效地址)指令是 movq 指令的变体,用来将某个有效内存地址写入对应寄存器,作用类似 C 语言的取地址运算符 &。这条指令可以为后面的内存引用产生指针。leaq 的目的操作数只能是寄存器。
在此之外,leaq 也常被用于进行一些简单的算术操作,如若 %rdx 的值被设为 $x$,则 leaq 7(%rdx, %rdx, 4), %rax 将 %rax 的值设为 $5x+7$,此时 leaq 的作用完全与有效地址计算无关。GCC 等编译器特别倾向于使用 leaq 指令处理简单的算术操作。
作为说明,下面这段 C 程序将会被编译成如下三条 leaq 指令实现的汇编代码;注意 x,y,z 对应的寄存器按顺序分别是 %rdi, %rsi, %rdx。
| |
| |
${\bf N{\scriptsize OTE}}.$ 注意 GNU assembler 使用
#处理单行注释。
之所以这样做,是因为 Intel 处理器有一个专门的地址运算单元,leaq 的运行不必经过 ALU,只需要单个时钟周期,显然比使用乘法指令 imul 要快得多。
练习题 3.6
| 表达式 | 结果 |
|---|---|
leaq 6(%rax), %rdx | $x + 6$ |
leaq (%rax, %rcx), %rdx | $x + y$ |
leaq (%rax, %rcx, 4), %rdx | $x + 4y$ |
leaq 7(%rax, %rax, 8), %rdx | $7 + 9x$ |
leaq 0xA(, %rcx, 4), %rdx | ${\tt 0xA} + 4y$ |
leaq 9(%rax, %rcx, 2), %rdx | $9 + x + 2y$ |
练习题 3.7
5 * x + 2 * y + 8 * z
3.5.2 一元和二元操作
一元操作符的操作数只有 1 个,可以是寄存器/内存位置。
二元操作符的操作数有 2 个,第一个操作数可以是立即数/寄存器/内存位置,第二个操作数可以是寄存器/内存位置;注意第二个操作数同时为源操作数和目的操作数。
练习题 3.8
| 指令 | 目的 | 值 |
|---|---|---|
addq %rcx, (%rax) | ${\tt 0x100}$ | ${\tt 0x100}$ |
subq %rdx, 8(%rax) | ${\tt 0x108}$ | ${\tt 0xA8}$ |
imulq $16, (%rax, %rdx, 8) | ${\tt 0x118}$ | ${\tt 0x110}$ |
incq 16(%rax) | ${\tt 0x110}$ | ${\tt 0x14}$ |
decq %rcx | %rcx | ${\tt 0x0}$ |
subq %rdx, %rax | %rax | ${\tt 0xFD}$ |
3.5.3 移位操作
移位指令先给出移位量,再给出要移位的量。其中,移位量可以是一个立即数或单字节寄存器 %cl(不能是其他寄存器),目的操作数可以是一个寄存器或内存位置。
当移位量为 %cl 时,具体的移位量由 %cl 的低 $m$ 位决定:当移位操作对 $w$ 位的数据进行操作时,$m$ 通过 $2^m=w$ 来确定。
例如:当 %cl 的值为 ${\tt 0xFF = 0b1111,1111}$ 时,根据使用的指令不同,分别有:
- 使用
salb指令时,操作数据长度为 8 位,此时有 $m = 3$,即位移量为低 3 位 ${\tt 0b111 = 7}$。 - 使用
salw指令时,操作数据长度为 16 位,此时有 $m = 4$,即位移量为低 4 位 ${\tt 0b1111 = 15}$。 - 使用
sall指令时,操作数据长度为 32 位,此时有 $m = 5$,即位移量为低 5 位 ${\tt 0b0001,1111 = 31}$。 - 使用
salq指令时,操作数据长度为 64 位,此时有 $m = 6$,即位移量为低 6 位 ${\tt 0b0011,1111 = 63}$。
移位指令中,sal,shl,sar,shr 指令分别代表算术左移、逻辑左移、算术右移、逻辑右移,其中算术左移与逻辑左移的效果是相同的;算术右移的效果为用符号位填充空位,逻辑右移的效果为用 0 填充空位。
练习题 3.9
salq $4, %rax
sarq %cl, %rax
3.5.4 讨论
可以看到上述算术/逻辑操作指令大多数可同时用于有符号和无符号运算,只有右移操作要求显式区分有符号和无符号数;这个特性也是采用补码运算作为有符号整数运算的比较好的原因之一。
考虑以下 C 语言代码将会被编译成的汇编代码:
| |
这里的每一句 C 源代码都紧密地对应一句或多句汇编指令。将其写成对应的汇编代码:
| |
汇编代码中有值得注意的以下两点:
- 使用了两条
leaq和移位指令来计算小的乘法。 - 因为
0x0F0F0F0F是一个双字长,因此使用andl和%edi参与运算。
练习题 3.10
| |
练习题 3.11
A. 将 %rdx 清零。这是因为对任何 $x$,有 ${\rm XOR}(x,x) = 0$。
B. movq $0, %rdx
C. 在 WSL(Ubuntu 20.04, Intel i5-3470) 平台上使用如下汇编代码编译目标文件:
| |
使用 objdump 反汇编得:
file.o: file format elf64-x86-64
Disassembly of section .text:
0000000000000000 <a>:
0: 48 31 d2 xor %rdx,%rdx
0000000000000003 <b>:
3: 48 c7 c2 00 00 00 00 mov $0x0,%rdx
000000000000000a <c>:
a: 90 nop
可见两条指令编码长度分别为 3 字节和 7 字节。
${\bf N{\scriptsize OTE}}.$ 此外,通过使用「生成 4 字节值并以寄存器作为目的操作数的指令会将高 4 字节置为 0」的特性,可以使用
xorl和movl指令进一步压缩长度。如:将如下汇编代码编译为目标文件:
1 2 3a: movl $0, %eax b: xorl %eax, %eax c: nop使用
objdump反汇编得:test.o: file format elf64-x86-64 Disassembly of section .text: 0000000000000000 <a>: 0: b8 00 00 00 00 mov $0x0,%eax 0000000000000005 <b>: 5: 31 c0 xor %eax,%eax 0000000000000007 <c>: 7: 90 nop可见
xorl和movl指令只分别需要 2 字节和 5 字节。关于「生成 4 字节值并以寄存器作为目的操作数的指令会将高 4 字节置为 0」这一特性的效果,可以使用
gdb进行测试:先编译如下代码:
1 2 3 4 5 6 7 8.section .text .globl _start _start: movq $0xABCDABCDABCDABCD, %rax xorl %eax, %eax movq $3, %rax xorl %eax, %eax nop使用如下指令进行编译(
--gstabs+参数用于保留符号信息,用于调试):
1 2as -o test.o test.s --gstabs+ ld -o test test.o使用
gdb进行调试,在_start处加断点,并使用i register <寄存器名称>打印寄存器的值:Copyright (C) 2020 Free Software Foundation, Inc. License GPLv3+: GNU GPL version 3 or later <http://gnu.org/licenses/gpl.html> This is free software: you are free to change and redistribute it. There is NO WARRANTY, to the extent permitted by law. Type "show copying" and "show warranty" for details. This GDB was configured as "x86_64-linux-gnu". Type "show configuration" for configuration details. For bug reporting instructions, please see: <http://www.gnu.org/software/gdb/bugs/>. Find the GDB manual and other documentation resources online at: <http://www.gnu.org/software/gdb/documentation/>. For help, type "help". Type "apropos word" to search for commands related to "word"... Reading symbols from testtest... (gdb) b _start Breakpoint 1 at 0x401000: file testtest.s, line 4. (gdb) run Starting program: /mnt/d/programming/tempanswertest/testtest Breakpoint 1, _start () at testtest.s:4 4 movq $0xABCDABCDABCDABCD, %rax (gdb) i registers rax rax 0x0 0 (gdb) s 5 xorl %eax, %eax (gdb) i registers rax rax 0xabcdabcdabcdabcd -6067004223159161907 (gdb) s 6 movq $3, %rax (gdb) i registers rax rax 0x0 0 (gdb) s 7 xorl %eax, %eax (gdb) i registers rax rax 0x3 3 (gdb) s 8 nop (gdb) i registers rax rax 0x0 0 (gdb) s Warning: Cannot insert breakpoint 0. Cannot access memory at address 0x1 0x0000000000401016 in ?? ()
3.5.5 特殊的算术操作
考虑两个 $w$ 位无符号整数 $x,y$ ($0 \leq x,y \leq 2^w - 1$),则有 $0 \leq x \cdot y \leq (2^w - 1)^2 = 2^{2w}-2^{w+1}+1$,也即 $x \cdot y$ 最多要用 $2w$ 位来表示;
同样地,考虑两个 $w$ 位有符号整数 $x, y$($-2^{w-1} \leq x,y \leq 2^{w-1}-1$),则有 $$ -2^{w-1} \cdot (2^{w-1}-1) \leq x \cdot y \leq (-2^{w-1})^2 $$ 即 $$ -2^{2w-2}+2^{w-1} \leq x \cdot y \leq 2^{2w-2} $$ 最多需要 $2w-2$ 位;但是,考虑到计算机内寄存器的数位长度通常以 2 为倍数进行倍增,可以认为无论有/无符号,$x \cdot y$ 均需最多 $2w$ 位进行表示。
因此,x86-64 指令集对长度为 128 位的八字(oct word)提供了有限支持。
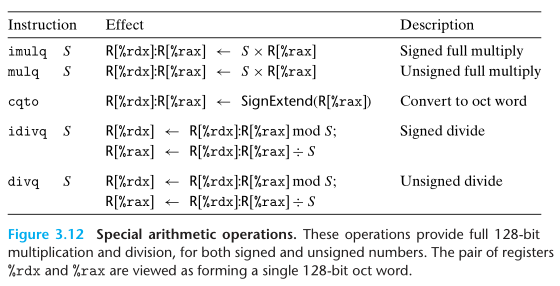
在这组指令中,%rdx 和 %rax 共同组成一个 128 位的八字。
在这组指令中,有两条单操作数乘法指令 imulq 和 mulq,都要求将一个参数预存在 %rax 中,并将乘积结果的低 64 位放在 %rax 中,将高 64 位放在 %rdx 中。同时,x86-64 指令集还提供一个双操作数乘法指令 imulq(与单操作数乘法指令名称相同),如图 3-10 所示;但运算结果只截取低 64 位,和 C 语言的无符号/补码乘法运算相同(参考 2.3)。在只截取低 64 位的情况下,无符号/乘法运算结果的二进制位表示是相同的,因此只需要一条指令即可处理。
${\bf N{\scriptsize OTE}}.$ 证明:$w$ 位的无符号乘法和补码乘法结果的二进制位表示相同。
考虑对位向量 $\vec{x} = [x_{w-1},x_{w-2},\cdots,x_0],,,x_i \in {0,1},,,i=0,1,\cdots,w-1$,
$\vec{x}$ 对应的无符号编码的值表示为 $$ x_u = \sum_{i=0}^{w-1}x_i2^i $$ $\vec{x}$ 对应的补码编码的值表示为 $$ x_t = -x_{w-1}2^{w-1}+\sum_{i=0}^{w-2}x_i2^i $$ 显然有 $$ x_u = x_t + x_{w-1}2^w $$ 因此,设 $x,y$ 是 $w$ 位无符号整数,则其对应的补码编码的值分别为 $x’ = x + x_{w-1}2^w$,$y’ = y + y_{w-1}2^w$。此时,考虑 $x’$ 与 $y’$ 的乘积截取低 $w$ 位的结果得:
$$ \newcommand{\modop}{,{\rm mod},} \begin{aligned} (x’ \cdot y’)\modop2^w &= [(x + x_{w-1}2^w) \cdot (y + y_{w-1}2^w)] \modop 2^w \ &= [(x \cdot y) + x \cdot y_{w-1}2^w + y \cdot x_{w-1}2^w + x_{w-1}y_{w-1}2^{2w}] \modop 2^w \ &= (x \cdot y) \modop 2^w \end{aligned} $$
证毕。
有/无符号整数除法指令 idivq 和 divq 只有单操作数版本,它们都将 %rax 作为被除数的低 64 位,%rdx 作为被除数的高 64 位;并把计算结果的商放在 %rax 中,余数放在 %rdx 中。
在有符号运算的情况,可以用指令 cqto 将四字符号扩展到八字:被扩展的低 64 位值放在 %rax 中,指令会根据其符号位自动填充 %rdx 中的高 64 位值。如果有符号除法指令中的被除数是一个 64 位的值,则需要提前用 cqto 将其符号扩展至 128 位;无符号除法中则需要手动将 %rdx 置为 0。
练习题 3.12
| |
3.6 控制
3.6.1 条件码
常用的条件码寄存器有如下几个:

图 3-10 中,除了 leaq 外的所有指令都会重新设置条件码寄存器。

此外,某些操作有一些特殊的行为:
- 逻辑操作,例如
xor,会将CF和OF设置为 0。 - 移位操作会将
CF设置为最后一个被移出的位,OF设置为 0。 inc和dec指令会设置OF和ZF标志,但是不会改变CF标志。
还有 cmp 和 test 两类指令会设置条件码但不修改任何其他寄存器:
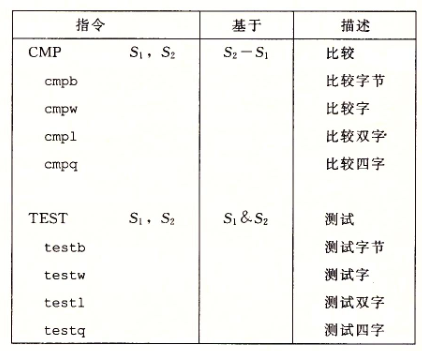
其中,cmp 指令和 sub 指令的行为是一样的,test 指令和 and 指令的行为是一样的。
当 test 指令的两个操作数相同时,可以用来判断一个值是负数,0,还是正数(例如,对 %rax 使用 testq %rax, %rax);test 指令也可配合一个掩码来指定测试一个值中的某些位。